在《建筑工程抗浮设计规程》(DBJ/T 15-125-2017)中,9.0.7 锚杆基础中单根锚杆抗拔承载力应按下列公式验算:
\(N_{t,max} \leq1.2 R_{ta}\)
而国标《建筑地基基础设计规范》(GB50007-2011)8.6.2规定.jpg)
.jpg)
一般的,仍按\(N_{t,k} \leq R_{ta}\)
一、问题的提出
根据上式,令\(f(\theta)=N_{t,k}/R_{ta}\),是否提出f(θ)为抗浮桩(锚杆)的利用率?即我们配桩,尽可能让计算桩反力与抗拔特征值接近。
二、结论
f(θ)为θ的函数(\(\theta={G_k \over N_{w,k}}\)),即,f(θ)受自重与水浮力比值的影响,其值不定,作为利用率指标,只有当两项目的θ相当时,比较才有意义,故f(θ)作为利用率评价指标不合适。f(θ)按抗浮国标计算和广东省标计算亦有差别。论证如下,
1.利用率应该有上限值,且为100%。
2.令\(f(\theta)=N_{t,k}/R_{ta}\),其理论上限是θ的函数(其中\(\theta={G_k \over N_{w,k}}\),Gk为建筑物自重和压重,Nw,k为水浮力),f(θ)为理想利用率。
3.忽略弯矩M的影响,\(N_{t,k}=N_{w,k}-G_k=(1-\theta)N_{w,k}\),
3.1 国标《建筑工程抗浮技术标准》(JGJ476-2019)在3.0.3处规定:
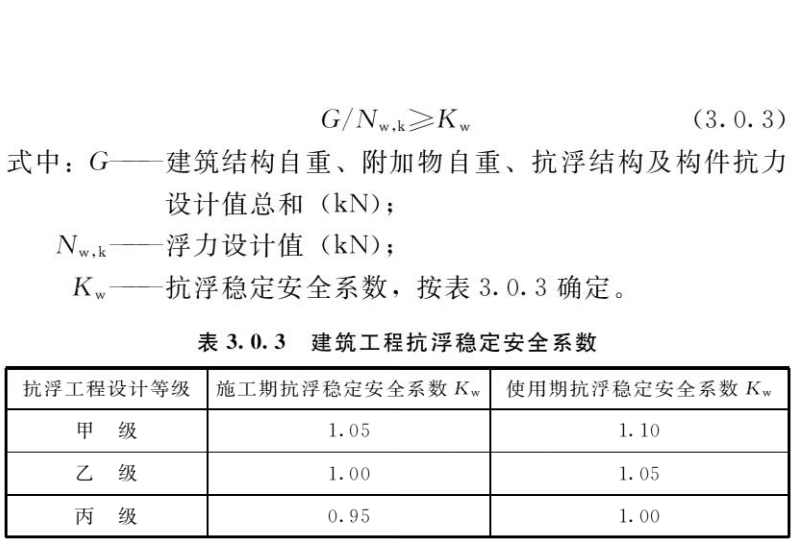
变换为\(G≥N_{w,k}*(γ_0K_w)\),其中G包括抗浮结构及构件抗力设计值。
\(R_{ta}=(γ_0K_w)N_{w,k}-G_k=(γ_0K_w-θ)N_{w,k}\)
\(f(\theta) = { 1- \theta \over \gamma_0\mathit{K}_w-\theta} \quad \quad(国标公式)\)
3.2 省标5.1.3 规定如下:

从上面两式对比,可知\(R_k\)不考虑\(γ_0K_w\)的安全系数,事实上抗拔特征值计算时,已考虑K=2的安全系数,原式等于\(N_{w,k} \leq { G \over \gamma_0K_w} +{ R_{tu} \over K}\)。
\(R_{ta}=N_{w,k}-{G_k\over (γ_0K_w)}=(1- { θ \over γ_0K_w})N_{w,k}\)
\(f(\theta) = { 1- \theta \over 1-{\theta \over \gamma_0\mathit{K}_w}} \quad \quad(省标公式)\)
令(γ0Kw)=1.1*1.1,即抗浮工程设计等级甲级。做y=f(θ)图表如下:
按省标计算f(θ)有上限值1.0,而按国标则上限值为0.826,按省标计算,f(θ)上限值可取到1.0,个人觉得更显合理。
三、抗浮桩(锚杆)利用率指标建议
1. 理想计算桩数,考虑重要性、抗浮稳定系数、水浮力、自重的影响,不考虑桩承载力取值离散性。
考虑理想计算桩数n:\(理想n*N_{t,k}=N_{w,k}-G_k\)
理想利用率\(f(\theta)=N_{t,k}/R_{ta}\)
\(理想n={N_{w,k}-G_k \over f(θ) *R_{ta}}\)
比如,甲级抗浮,\(γ_0K_w=1.1*1.1\),设\(\theta={G_k \over N_{w,k}}=0.5\),按国标或省标求出f(θ)=0.704或0.852,\(理想n={N_{w,k}-G_k \over f(θ) *R_{ta}}\)。
2.定义抗浮桩(锚杆)的布置效率,采用实际布置桩数与理想计算桩数的比值的倒数。布置效率反应桩承载力取值的离散性。
\(\eta_{布置效率}={理想n \over 实际n}\),假设预算桩数采用理论桩数*1.3,布置效率为77%。
3. 定义桩反力与承载力特征值比为桩实际利用率\(\rho_{实际利用率}={N_{t,i} \over R_{ta}}\),其中,\(N_{t,i}={N_{w,k} - G_k \over 实际n}\)
桩实际利用率=布置效率*理想利用率,即\(\rho_{实际利用率}=\eta_{布置效率}*f(\theta)\)
4.用布置效率作为设计评价指标更为合理,而实际利用率可用来反应投资成本。
四、两本规范差别的其他说明
1.《建筑结构可靠度设计统一标准》GB50068-2018,4.1.1规定,结构及构件稳定计算属于承载力计算范畴,应考虑结构重要性系数。而《建筑工程抗浮技术标准》(JGJ476-2019)在3.0.3处未表达重要性系数,而重要性系数取值在7.1.8描述,不连贯。
省标《建筑工程抗浮设计规程》(DBJ/T 15-125-2017)则在抗浮稳定计算公式中明确表达重要性系数(见5.1.2-5.1.3)。
2.国标3.0.9规定抗浮稳定性验算作用效应按承载力极限状态作用的基本组合,分项系数取1.0。6.3.7规定总抗浮力计算使用组合系数中,区分对抗浮稳定有利不利,事实上,抗浮构件包括自重,方向总是与水浮力方向相反,该提法存疑。6.4节提出总抗浮力标准值概念,与3.0.9不呼应。
省标在3.0.2明确抗浮稳定性验算及抗拔构件的承载力验算采用安全系数法,5.1节抗浮稳定性验算公式与之呼应。
3.建议广东省项目仍采用省标,根据\(理论n={N_{w,k}-G_k \over f(θ) *R_{ta}}\),采用省标可降低理论桩数。
Last Modified·2021年11月11日 15:27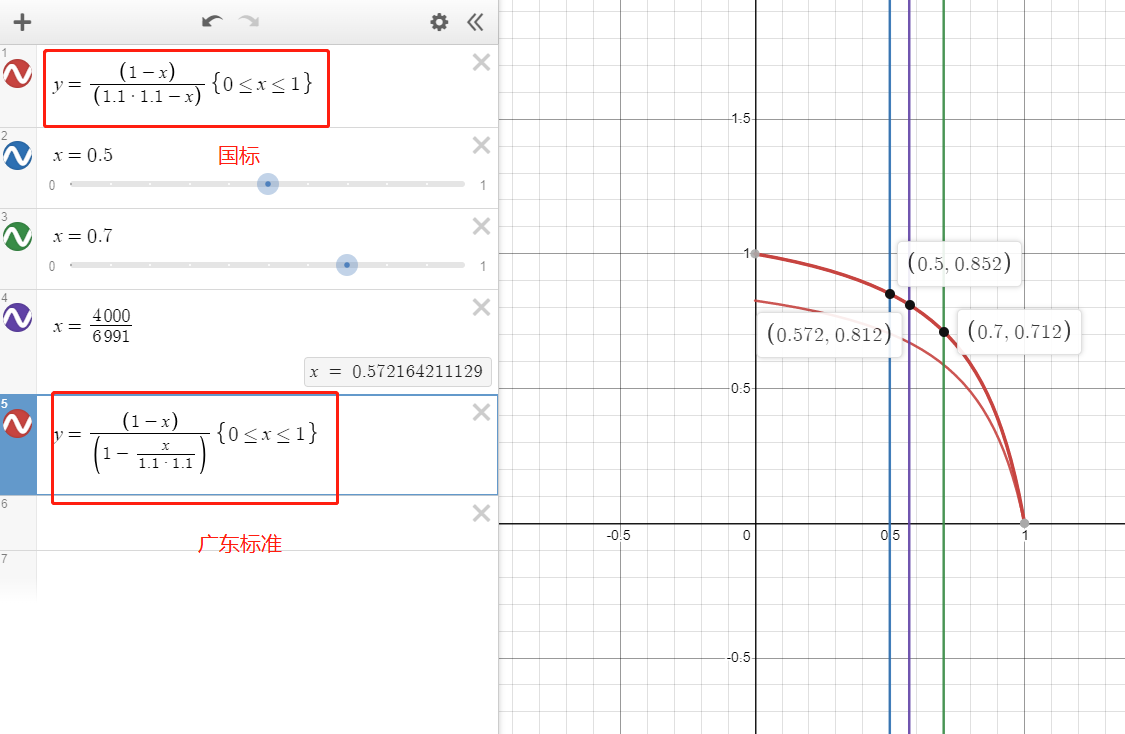
您尚未登录,请先登录才能评论。