此文根据豆包生成
我们来完整证明用 \(\frac{1}{n}\)定义的样本方差 \(s^2 = \frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2\)是有偏的。
1. 展开平方项
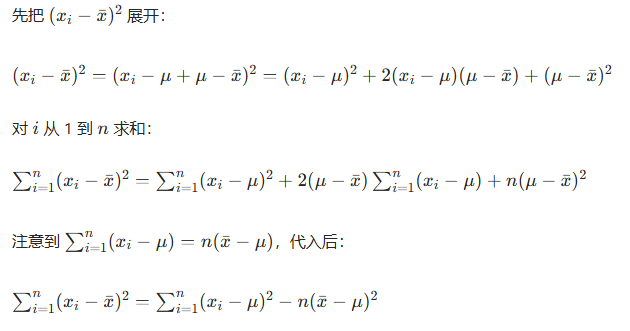
2. 两边取期望
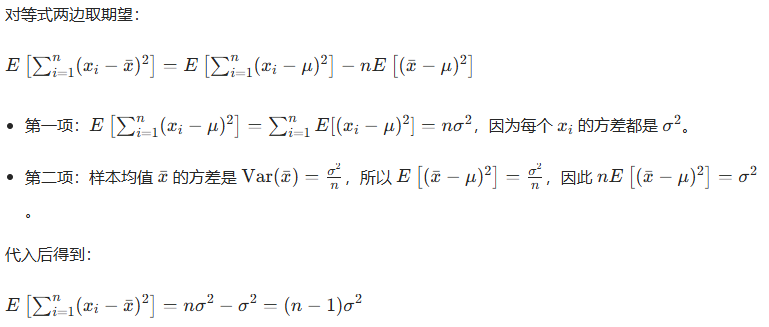
3. 计算 \(E[s^2]\)
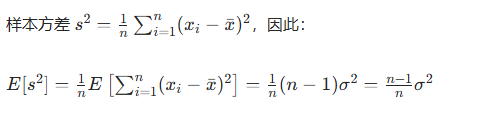
4. 结论

5. 引论:样本均值的方差
5.1 基本设定

5.2 方差计算

此文根据豆包生成
我们来完整证明用 \(\frac{1}{n}\)定义的样本方差 \(s^2 = \frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2\)是有偏的。
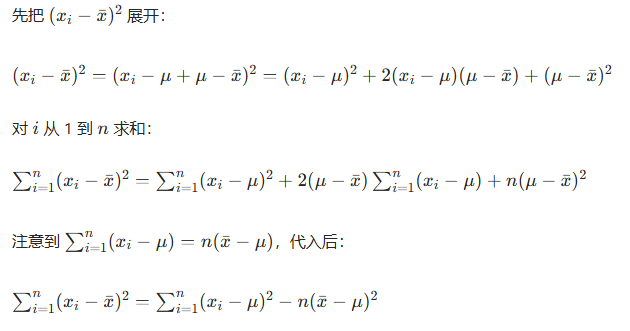
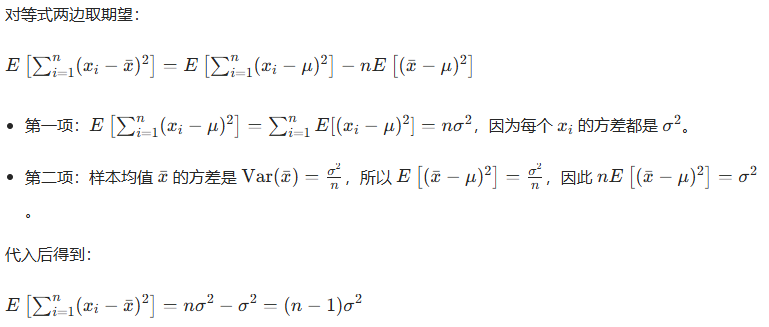
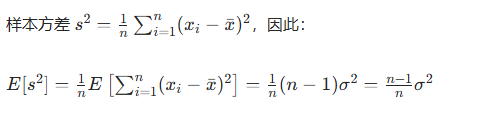



您尚未登录,请先登录才能评论。