行车道板的计算
《公桥混规》 4.1.2
- 简支板的计算跨径应为两支撑中心之间的距离。与梁肋整体连接的板,计算弯矩时其计算跨径可取两肋间的净距加板厚,但不大于两肋中心之间的距离。此时,弯矩可按以下简化方法计算:
- 支点弯矩
\(M = -0.7 M_0\) (4.1.2-1)
- 跨中弯矩
1)板厚与梁肋高度比不小于1/4时
\(M = +0.7 M_0\) (4.1.2-2)
2)小于1/4时
\(M = +0.5 M_0\) (4.1.2-3)
与梁肋整体连接的板,其计算剪力时的计算跨径可取两肋间净距,剪力按计算跨径的简支板计算。
- 简支板单位宽度的跨中弯矩\(M_0\)
\(\gamma_0 M_0 = \gamma_0(\gamma_GM_{0g} + \gamma_{Q1}M_{0p} )\)
\(M_{0g}=\frac1{8}\mathrm{g}l^2\)
作用在跨中的分布宽度为b的\(M_{0p}\)计算:
\(\because N_支=\frac {bp} {2}=\frac {P}{4a}\) ,\(p=\frac {P}{2ab}\)
\(M_{0p}=(1+\mu) \left ( N_支 \frac{l}{2} - \frac{N_支}{2} \frac{b}{2} \right )\)
\(\therefore M_{op}=(1+\mu)\frac{P}{8a}(l-\frac{b}{2})\)
注: 1. 上式负数项为轮压均匀分布的影响。
2. 通常由弯矩控制设计。
支点剪力:
\(V_s=\frac1{2}\mathrm{g}l_0+(1+\mu)(A_1y_1+A_2y_2)\)
合力面积A和支点剪力影响线竖标值如图所示:
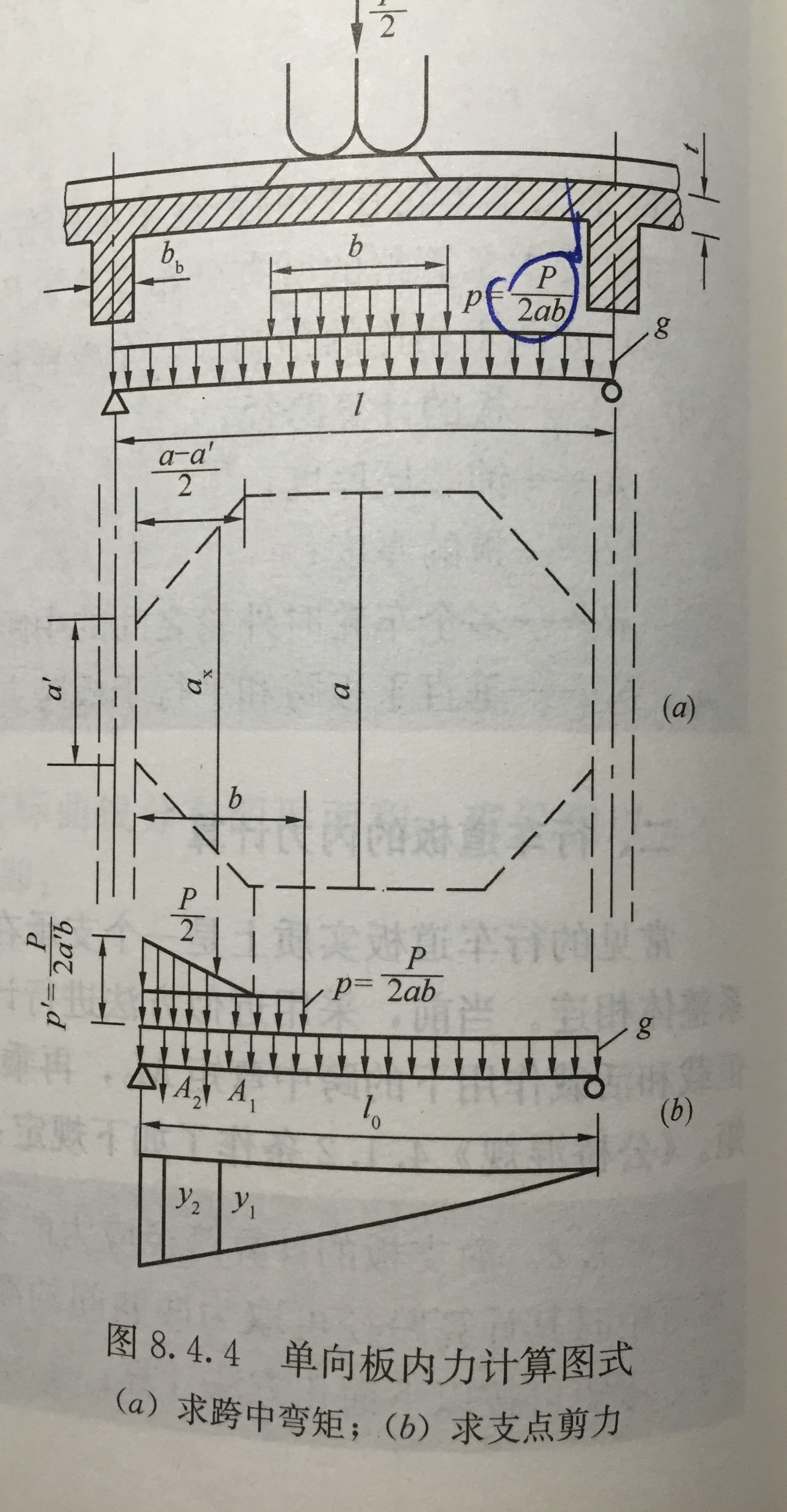
隐含条件为b大于\(\frac{a-a'}{2}\),大致为:\(l < 6(b_1+2h+\frac{t}{2})\),代入常见数值,得\(l<3.1m\)
Last Modified·2017年6月22日 09:44
您尚未登录,请先登录才能评论。