自然底数e的解读,在知乎上,张英锋的回答获得6万+的赞,值得分享其解读。并部分摘录:
好问题,让我尝试不用公式,用跨越7000年人类文明的方式,来解读e的自然之美,争取有中学基础的人就能看懂。
e有时被称为自然常数(Natural constant),是一个约等于2.71828182845904523536……的无理数。
以e为底的对数称为自然对数(Natural logarithm),数学中使用自然(Natural)这个词的还有自然数(Natural number)。这里的“自然”并不是现代人所习惯的“大自然”,而是有点儿“天然存在,非人为”的意思。就像我们把食品分为天然食品和加工食品,天然食品就是未经人为处理的食品。
但这样解读“自然”这个词太浅薄了!为了还原全貌,必须穿越到2500多年前的古希腊时代。(你也知道,穿越剧都很长(>﹏<),不喜欢长篇大论的,可直接跳到后面看结论。)
- “自然”的发明
我们知道,人类历史上曾出现过很多辉煌的文明,例如大家熟知的四大文明:古巴比伦、古埃及、古印度河以及古代中国。
但是要说谁对现代文明的影响最大?对不起,四大文明谁都排不上!真正对现代文明影响最大的是古希腊文明,特别是古希腊的哲学、科学思想,是整个现代文明的源头和基石。这里并不是要贬低四大文明,现代文明也从各文明继承了大量的文化遗产,只是相比古希腊要少很多。
现代人的基础教育,无论是什么国家、什么社会制度、什么民族,在教科书里除了介绍自己的古代成就外(如四大发明),还会大篇幅的介绍古希腊的科学、哲学思想,来启蒙学生的心智,这是跨越国界的共同做法。
大家都这样做的原因,就是因为古希腊哲学家发明了科学的思维方法和“自然”(Natural)这个词,在理论中用自然来取代具体的神灵,这是人类文明史上划时代的发明。如果没有这个发明,现代文明可能还会晚出现数千年,所以这是至关重要的进步。
在古希腊文明之外的古文明里,人们解释世间万物的运行时,总是要引入神灵等超自然、拟人化的因素。例如,得病了就认为鬼神附体,洪水泛滥就认为天神发怒,石人一出天下就可以造反了,总有一个超自然的神灵在操纵万物的运行。人们偏爱形象而戏剧化的解释,拟人化的神灵恰恰具有形象、戏剧化的特点,最易于接受和传播。现代喜欢希腊神话的人数,也远多于喜欢希腊哲学的。电视里最流行各种奇幻故事,例如狼人、吸血鬼什么的。古代人也一样,不同的是我们知道这是假的,古人则认为是真的,这成为他们理解世界运行的思维定势。
直到公元前624年,泰勒斯的出现,才第一次用自然取代神灵的位置。

泰勒斯被称为“科学和哲学之祖”、“科学之父”、“哲学史上第一人”!(还有比这更牛的称号吗?)
其实泰勒斯是个多神论者,他认为神是存在的,是神让万物有了自己内在的规律。但解释万物的运行,不能靠凭空的制造故事,要靠坚实的证据来发现这些规律,并用理性的方法解读。这就是泰勒斯的最大贡献,开创了一套认识世界的全新思维方法,他关注的是证据、规律、理性,而不是神。
尽管泰勒斯提出的理论现在看起来很粗糙。但是人们不再需要像宗教一样,把旧理论看成是不可否定的权威结论。只要有坚实的新证据和理性的推理,旧理论可以被修改或推翻,更好的理论就可以建立起来。这是一种可靠的、可进化的理论体系。相反,宗教是停止进化的、只能膨胀的理论体系,例如你只能解读圣经,但不能否定圣经。
后来的希腊哲学家不断借鉴和发展泰勒斯的理论,建立了“自然”(φύσις)的概念,“自然”代表万物因为本源而发生自然而然的变化。赫拉克利特还引入了逻各斯(希腊语:λόγος,英语:Logos)的观点,用以说明万物变化的规律性。逻各斯原来是指语言、演说、交谈、故事、原则等,这里的逻各斯则主要指一种尺度、大小、分寸,即数量上的比例关系。后来对数的发明人纳皮尔就用Logos和arithmos(算法)创造了单词Logarithm 来命名对数法,经过后人简化变成了对数符号log。
几乎和古希腊同一时代,春秋战国时代的诸子百家也提出过一些相似的思想,例如老子的道。但很可惜,这种蓬勃发展的思想爆炸因为诸多原因戛然而止,只是昙花一现。但是限于篇幅,这里不再展开,请到最后的推荐阅读中了解。
- “自然”与美
古希腊的学者还给“自然”赋予美的含义,他们认为规律性就是一种和谐感,数学的比例是种超越肉体感官、只能靠心智才能领悟到的美。毕达哥拉斯就是其中最极端的代表,他对数学美的狂热追求超过了偏执的程度,美像神一样不可冒犯,毕达哥拉斯主义走向了科学的反面,成了宗教。
这种宗教的狂热驱动他和信徒们不断的去挖掘“自然”之美,并在数学之外的音乐、建筑、雕刻、绘画等领域发现了大量的比例关系,最有名的是毕达哥拉斯定理(中国叫勾股定理)。毕达哥拉斯认为所有图形中,圆是最对称的,所以圆是最完美的图形。参见毕达哥拉斯学派美学思想(朱光潜)
- “自然”思想的意义
雷军说得好,“在风口上,猪都会飞”!就像乔布斯开启了移动互联网时代,泰勒斯则开启了古希腊哲学时代。
古希腊时代是一个科学、哲学大爆炸的时代,原本黑暗的天空中突然爆发出无数的新星:赫拉克利特、毕达哥拉斯、德谟克利特、苏格拉底、柏拉图、亚里士多德、阿基米德、欧几里得、希波克拉底等等,都因为得益于这套思维方法,发现了大量的自然规律,成为各学科领域里开天辟地的先贤。
古希腊人还把自然的概念引入社会领域,来分析社会中的现象和规律。例如亚里士多德就曾经激烈的抨击借贷,认为在所有赚钱方法中,利息是最不自然的。
以自然作为基础,会比人为强制规定作为基础更稳定和可靠。
例如:
英尺(foot)的长度就是根据人的脚长来人为规定,人的脚长差异太大,历史上英尺发生过很多次变化,不稳定,这是不自然的。
而海里的长度则接近自然,如下图,海里是根据地球周长计算的,是1角分的长度,变化就极小。
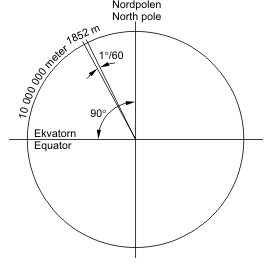
对比之下,宗教等理论体系的基石并不是自然的,靠的是强制手段来确立的权威,这是不稳定的。当强制手段不再有效时,就会使宗教分裂成各种教派。
自然思想不同于宗教,靠的是坚实的观察证据和理性思维,任何人都可以反复验证,具有可证伪性。这样打下的基础就非常的稳固。正是这种稳定性和可靠性,古希腊思想被越来越多的人所接受,对后人产生了巨大的影响,几乎奠定了现代所有科学领域的基础。
经过2500多年的不懈努力,终于在古希腊文明所铺就的最稳固基石上,人类建立起了现代文明的宏伟大厦。
- 自然数中的“自然”
古希腊认为像1、2、3这样的数,是事物本身就有的属性,可以用来描述日常事物的数量和顺序,无需过多解释,就是3岁小孩也能快速理解,所以这些数被称为自然数(Natural number)。
但这种朴素的自然观限制了数的范围,无法解释0,负数、分数、小数等数。古希腊人认为这些数并不自然,是人为了计算而发明出来的,不是自然的数。
毕达哥拉斯就非常厌恶无理数,无理数的不规律破坏了和谐美。他的门生希帕索斯Hippasus就是因为发现了√2并公布出去,居然被毕达哥拉斯以渎神的罪名被淹死了,这被称为数学史上的第一次數學危機。后人认为毕达哥拉斯也发现了黄金分割率,但因为也是无理数,所以一直秘而不宣。
现代我们知道,没有受过基础数学教育的人要想理解这些数,不仅需要了解更复杂的概念模型,还要熟悉加、减、乘、除等运算方法,只有这样才能完全明白。而更复杂的数,例如无理数、代數數和超越數,也需要了解更复杂的运算。
我们的主角e,就是超越数,既然理解e的含义需要理解相关的运算,而这些运算最早都和利息有关,所以我们继续穿越。从古希腊再往回穿越4000年,穿越到7000年前的苏美尔文明时代。
- 利息的发明
7000年前,美索不达米亚的苏美尔人因为发达的农业和贸易,建立起人类最早的文明和城市,参见问题《为什么会有国家?》。
苏美尔人也第一个发明了利息,一起通过一个虚构的小故事来理解利息的起源:
- 农民张三经常去城市卖粮食、换日常用品,他发现城里人很喜欢羊奶,这是一个商机!
- 但是他自己没有母羊,也买不起,于是他找到牧羊人王二小,想租借他的母羊。
- 张三想用大麦作为每年母羊的租金,但王二小想了想,不想把母羊租给他。
- 因为母羊每年都生羊羔,把母羊给张三,虽然有租金,但羊羔的收益就没了。
- 张三明白了王二小的顾虑,就承诺他只用母羊产奶,如果母羊生下羊羔,羊羔还是归王二小。
- 王二小认为这样才比较划算,于是就答应了租借母羊。
- 张三和王二小到神庙,要在神的见证下订立合同。
- 公证人用楔形文字把债务合同刻在了泥板上,并明确了租金和羊羔的归属。
羊羔收益成为租借者的应得利润,这很公平,也很自然。
后来人们发现借钱也应该给羊羔收益,因为这笔钱如果用来买母羊,每年都会有羊羔收益。所以钱借给贷款者,他除了要归还本金,还要归还这笔钱本应获得的羊羔收益。
这个羊羔收益就成为了后来我们熟知的利息,在苏美尔文字中,利息的单词mas原本是牲畜幼崽的意思,随着时间的推移,利息的含义逐渐和牲畜没有了关系。这和我们汉字中货币、宝贝、财产等词中都含“贝”字是一样,因为海贝就是3000多年前夏商时代流通的货币。
历史上每次新能源的普及都会引发人类社会革命性的进步,利息就是一种革命性的新能源发明,只是这次驱动的不是机器,而是人。
利息的价值就在于其巨大的激励作用,驱动人们把自己的资源拿出来,分享给其他人使用。利息的激励模式也迅速在实物、粮食、金银等资产借贷上得到普及。金融领域的第二大创新(第一是货币)就这样诞生了。
4000多年前的《埃什嫩那法典》(The Law of Eshnunna)中就有了对利息的规定:
每1谢克尔<白银>(180粒大麦)的利息是36粒大麦(即利率为20%);
每300塞拉(sila)<谷物>的利息是100塞拉(即利率为33.33%)。
激励机制设计在经济、管理、教育等领域有着核心动力的关键作用,设计好了就可以把人的自身潜能释放出来,这一点,喜欢玩游戏的都有切身体会。正是知乎的激励机制设计的好,我这篇超长文才写得出来。XX问答类网站无法让用户做到,是因为他们激励的方向是数量,而不是质量。
尽管利息能激励交换,但人们对利息还是有着爱恨交加的复杂感情:当急需钱时,人们焦急的不惜一切代价筹钱;等到终于借到钱,需要还利息时,人们又开始愤愤不平。
柏拉图就曾经主张,人们应该只还本金,不要归还利息。参见古希腊的债务危机
他的学生亚里士多德在《政治论》一书中也激烈的抨击利息,认为在所有赚钱方法中,利息是最不自然的。
And this term interest, which means the birth of money from money, is appliedto the breeding of money because the offspring resembles the parent. Wherefore of an modes of getting wealth this is the most unnatural.
来源:http://classics.mit.edu/Aristotle/politics.1.one.html
每个时代的人们都有他们思想的天花板,亚里士多德的天花板就是不能接受金钱可以像生命一样增殖。他认为这是荒诞的、不是钱原来的属性、是不自然的。但如果他知道利息的起源,明白利息在经济系统中的推动作用,他可能会改变观点,整个人类经济和政治史都会彻底改写了。
柏拉图和亚里士多德并不是第一个站出来抨击利息的人,但是他们在历代学者和政治精英中的巨大影响力,这些观点后来成为了社会的主旋律,后世的社会现象,例如中世纪教会禁止收息放贷、犹太人被歧视迫害,以及马克思的共产主义思想,都和柏拉图、亚里士多德有着一脉相承的关系。
好了,先从历史里出来一会儿,让我们来看一下利息和e的关系。
- 利息中的e
e和圆周率π都是超越数,π的含义可以通过下图的割圆术来很形象的理解。
假设等边形的对角线长为1,只要等边形的边足够多,算出来的周长就可以越来越接近圆周率π。
但是解释e的含义却很难找到这样直观的例子,阮一峰翻译的文章《数学常数e的含义》说的很好,只是公式太多,并不直观。
幸好我在原文《An Intuitive Guide To Exponential Functions & e》中找到了很直观的图,只要理解了这个例子,e的含义就明白了。
假设你在银行存了1元钱(下图蓝圆),很不幸同时又发生了严重的通货膨胀,银行存款利率达到了逆天的100%!
银行一般1年才付一次利息,根据下图,满1年后银行付给你1元利息(绿圆),存款余额=2元
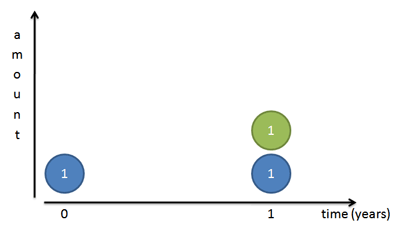
银行发善心,每半年付利息,你可以把利息提前存入,利息生利息(红圆),1年存款余额=2.25元
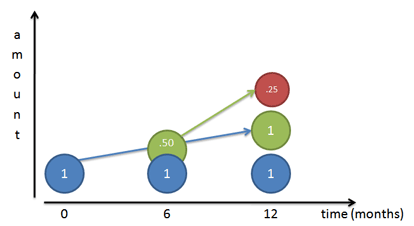
假设银行超级实在,每4个月就付利息,利息生利息(下图红圆、紫圆),年底的余额≈2.37元
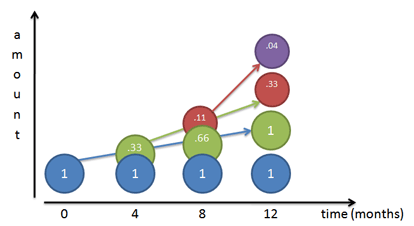
假设银行人品爆发,一年365天,愿意天天付利息,这样利滚利的余额≈2.71456748202元
假设银行丧心病狂的每秒付利息,你也丧心病狂的每秒都再存入,1年共31536000秒,利滚利的余额≈2.7182817813元
这个数越来越接近于e了!
哎呀!费了半天劲也没多挣几个钱啊!
对!1元存1年,在年利率100%下,无论怎么利滚利,其余额总有一个无法突破的天花板,这个天花板就是e,有兴趣可以用这个网上计算器算一下。
我们和圆周率再做个对比:
- 多边形的边数和利滚利的次数是相似的。
- 对角线为1的n边等边形,n趋于无穷,周长就无限接近于π,即π是周长的最大值。
- 年利率为1(100%)的1元存款,利滚利的次数n趋于无穷,存款就无限接近e,即e是存款的最大值。
换种表述方法:
- 每个完美的圆,其周长都是π的倍数;
- 每个理想的存款,其余额都是e的倍数。
这里停一停,你好好体会一下。
按照自然的观点,如果圆是最美的,那最赚钱也是最理想的。
有人问了:为啥银行不每秒返利息呢?这样就不是100%回报率,而是171.8%了,还我的71.8%!
银行哭到:臣妾做不到啊!!!
以上是意淫,银行不会这样发利息,洗洗睡吧,下面这个案例才比较现实。
- 利息的逆运算
还是从一个虚构的故事开始:
- 有一土豪要去银行存入大额存款,比如存1元。
- 银行经理推荐他投资理财产品,因为年利率高达100%,按照指数运算,bla bla bla……
- 但土豪的数学只有小学水平,听不懂有点烦,就问投资多长时间才能到10倍,100倍,1000倍?
- 经理有点懵,土豪不按常理出牌啊!
- 一般人都是根据存款时间问收益,例如收益第1年多少、第2年多少、第3年多少……
- 土豪居然逆向思维,根据收益问时间,多少年2倍,多少年5倍,多少年10倍!
- 不愧是老板,不问过程,只问结果!
- 于是经理就从第1年开始算,把10年内每年的收益都算出来,列成一个收益列表,如下图:
- 然后再找出收益最接近10倍,100倍,1000倍的年份指给土豪
- 土豪一看第4年、第7年、第10年就肯定超过预期收益,非常高兴!
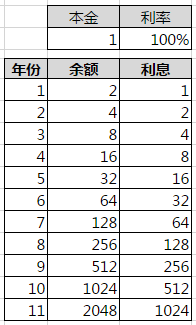
经理用这张表查找收益,再找到最接近收益的大体年份的过程,就是利息的逆运算,是最简单的对数运算,这个表就是对数表的雏形。
其实这和我们根据加法表进行减法运算、根据乘法表进行除法运算是同一个道理。
例如知道了\(3\times 7=21\),就可以很快知道\(21\div 3\)的除法逆运算结果了。
好了,放松一下大脑,继续回来穿越历史。
- 对数发明的历史
据说4000多年前,古巴比伦时代的人们就发明对数和对数表了,但因为我没找到资料证实,只能从近代开始。
16、17世纪,英、法加入了大航海的行列,开始了美洲殖民地的开拓,远洋贸易变得日益频繁。那时的人们已经知道地球是球形,大海上船只的位置靠经纬度来确定。
纬度测定很容易,几千年前人们就知道,通过测量北极星的仰角,可以估算出船已经在南北方向航行了多远。但是经度的测量不是一般的困难。在茫茫的大洋上,如果无法准确测定船只的经度,代价会极为高昂。
1707年,四艘英国战舰击败法国地中海舰队回航,10多天的浓雾让舰队完全迷失,因为算错经度,舰队触礁,两千名士兵死亡。1714年英国悬赏2万英镑(相当于现代的2000多万人民币),寻求精确测得经度的方法。
对于商人来说,与市场上的同类对手竞争,谁的航海定位越准确,意味着风险越低、利润越高。
对海军也是,同样的战舰,定位越准确,航行的时间越短,在战争中速度往往是决胜的关键。
经度的精确测量问题直到18世纪才得到有效解决,这归功于约翰·哈里森发明了高精度机械钟表。这段历史还被拍成了电影和记录片,推荐一本精彩的书《经度:一个孤独的天才解决他所处时代最大难题的真实故事》和罗辑思维的节目《击溃牛顿的钟表匠》。
其中,对数的发明人就是約翰·納皮爾。
纳皮尔是天文学家、数学家,在计算轨道数据时,也被浩瀚的计算量所折磨。
"看起来在数学实践中,最麻烦的莫过于大数字的乘法、除法、开平方和开立方,计算起来特别费事又伤脑筋,于是我开始构思有什么巧妙好用的方法可以解决这些问题。"
--约翰·纳皮尔,《奇妙的对数表的描述》(1614)
《e的故事:一个常数的传奇 》
但纳皮尔不是一般人,不想像IT民工一样苦逼的重复劳动,于是用了20年的时间,进行了数百万次的计算,发明了对数和对数表,堪称学霸中的战斗机。
为了理解对数计算的优势,我们通过案例来说明,下面的表格里有两个数列:

第2行是2的倍数,他们是等比的;
要计算第2行的等比数列中任意两个数的乘积,例如\(16\times 64\);
先到第1行的等差数列,寻找对应的数,16对应4,64对应6;
然后做加法,\(4+6=10\),再查找10所对应等比数列的1024;
得到计算结果就是\(16\times 64=1024\)
借助这个表,仅靠心算就可以用\(4+6=10\)的加法,完成麻烦的16×64乘法。
同样也可以进行除法变减法的运算,把\(1024\div 128=\),变为\(10-7=3\),对应结果为8。
把这个表变的更长,就可以计算数值更大的乘法,这个表就是极度简化的对数表。
以上仅仅是对数的优点之一,对数的易于计算,大大减少了数学家、天文学家的计算量。
拉普拉斯认为“对数的发现,以其节省劳力而延长了天文学家的寿命”
伽利略说过“给我空间、时间及对数,我就可以创造一个宇宙。”
如果把对数表的数列设计成尺子,就成了计算尺。有兴趣可以读果壳网的《如果没有计算器,我们就用计算尺吧》

- 微积分中的e
有人说:我不懂微积分,估计看不懂!
没关系!你可以这样理解,积分是升维的过程,微分是降维的过程。
例如
把一张张纸叠起来变成厚厚的词典,这是从2维变成3维的升维,这是积分;
把一大块羊肉,切成一片片羊肉片,就是从3维为变2维的降维,这是微分。
在微积分中,底数为e的指数函数\(e^{x} \),其导数还是这个函数\(e^{x} \),也就是不论求多少次导数,其导数就像一个常量一样永远是恒定的。不知道别人的感觉如何,反正我第一次知道时是很惊奇的。
举个例子:
西瓜都切过吧?
无论你怎么切一个实心球,其横截面都是圆面,也就是3维降2维,还是和圆有关。
2维的圆面也是有很多1维的同心圆组成,也就是2维降1维,还是和圆有关。
如上所说,球被降维了2次还是和圆有关,π这个常数你是甩不掉的。
这一点对更高维度的球也适用,参见n维球面。
\(e^{x} \)也是这样,而且比球面更厉害
无论如何降维,\(e^{x} \)总是老样子,一点儿都没变!
就好像你切掉孙悟空的一部分,你以为是一小片肉,睁眼一看,居然是另一个孙悟空,而且一样大!
这种自相似或全息性太匪夷所思、太好玩儿了!
大刘!我知道怎么化解《三体》外星人的降维攻击了!
下面就是\(e^{x} \)在直角坐标系中的样子
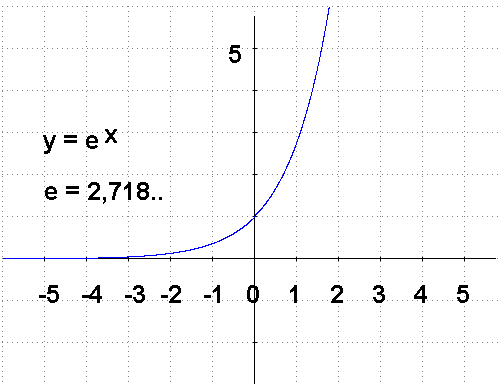
- 美妙的螺线
在上面的部分中,指数函数\(e^{x} \)的美并没有真正的体现出来。
让我们换一个视角看,你一定会大吃一惊。
我们知道二维坐标系除了直角坐标系外,还有一种常用的是极坐标系,如下图
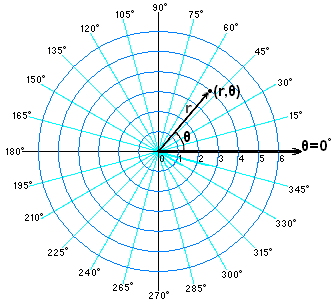
我们把指数函数\(e^{x} \)换成极坐标,就变成了\(e^{\theta} \),\(\theta\)是点与极轴的夹角。
这时的指数函数就会变成下图的样子,这个螺线叫对数螺线(Logarithmic spiral),又叫等角螺线。
之所以叫等角螺线,是因为在极坐标中,螺线和射线的夹角始终是一个固定夹角,如下图所示,蓝线每次穿过射线时,其夹角是固定的,也就是等角,我们在后面会用到这个等角特性。

有人说:等等!我好想在哪里见过这货?

不对,这个图,好像有什么东西乱入了!>_<#
这就是人体曲线,啊不,是斐波那契螺线,网上很流行玩这种摄影,都快被玩坏了。
其特点是前两个数加起来就是下一个数,例如
1+1=2
1+2=3
2+3=5
……
34+55=89
……
用这些数画出来的半圆,可以拼接成下面的螺线形状,这就是斐波那契螺线。
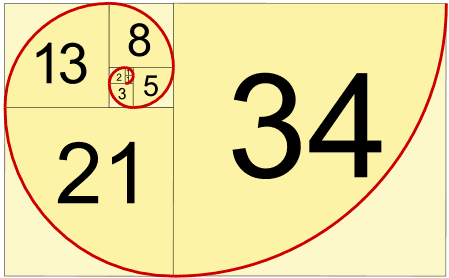
套用在美女图片上就可以这样玩,虽有过度解读之嫌,但可以获得极好的传播效果。

有趣的是这个数列还和黄金比例有关,例如55/34≈1.6176,接近黄金分割比例1.618,数列的数字越到后面,结果就越趋近于黄金分割这个无理数,如下图
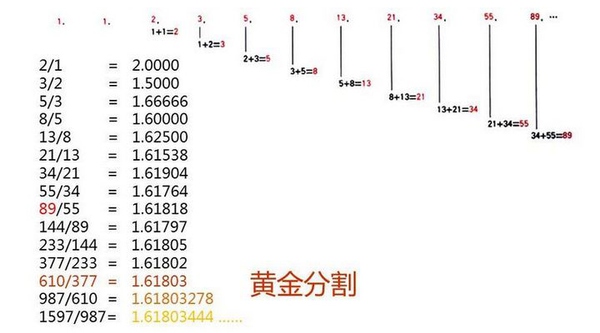
不过斐波那契螺线仅仅是对一种叫黄金螺线(Golden spiral)的近似,黄金螺线是一种内涵黄金分割比例的对数螺线\(e^{\theta} \),下图红色的才是黄金曲线,绿色的是“假黄金螺线”(斐波那契螺线),近似却不重合。

很多科学家发现对数螺线\(e^{\theta} \)在自然界中广泛存在。从大如星系、台风,到小如花朵、海螺……宇宙中到处都是对数螺线\(e^{\theta} \)的身影

原来e以这种特殊的方式隐藏在自然之中。需要注意的是,这不是e被称为自然底数的原因,这和大自然没太大关系。
为什么自然界中存在这么多的对数螺线呢?
因为对数螺线具有等角性,受环境影响,很多直线运动会转变为等角螺线运动。
我们以飞蛾扑火为例
亿万年来,夜晚活动的蛾子等昆虫都是靠月光和星光来导航,因为天体距离很远,这些光都是平行光,可以作为参照来做直线飞行。如下图所示,注意蛾子只要按照固定夹角飞行,就可以飞成直线,这样飞才最节省能量。

但自从该死的人类学会了使用火,这些人造光源因为很近,光线成中心放射线状,可怜的蛾子就开始倒霉了。
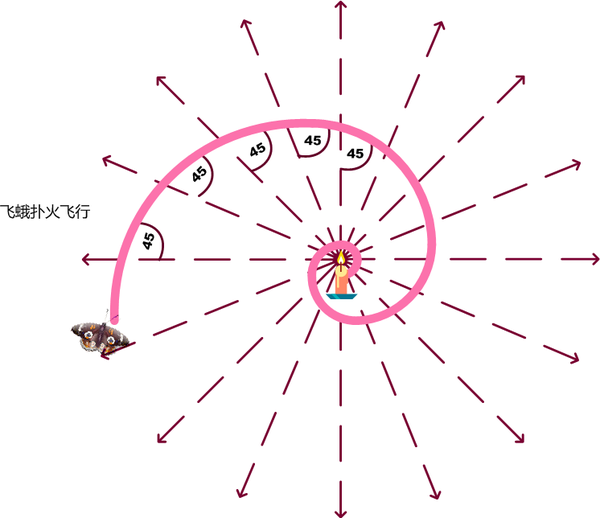
蛾子还以为按照与光线的固定夹角飞行就是直线运动,结果越飞越坑爹,飞成了等角螺线,最后飞到火里去了,这种现象还被人类称为昆虫的正趋光性。
蛾子说:
趋你妹的光啊,傻瓜才瞪着光飞,不知道会亮瞎眼啊?!!
我们完全被人类误导了,亿万年才演化出的精妙直线导航方法,被人类的光污染干扰失效了!
不用假慈悲的飞蛾扑火纱罩灯了,凸(#‵′)凸,赶紧把灯关了吧!
注意下图飞虫都在做螺线飞行,如果昆虫有趋光性。直飞不是更好吗?

不要以为只有蛾子会这样,人在用指南针导航时也有同样的问题,因为篇幅太长就不展开了,有兴趣请移步《既然昆虫有趋光性,为什么昆虫不齐刷刷地奔向太阳?》。
根本原因是原来作为参考的平行场变成了中心发散的场,导致直线运动变成了螺线运动。
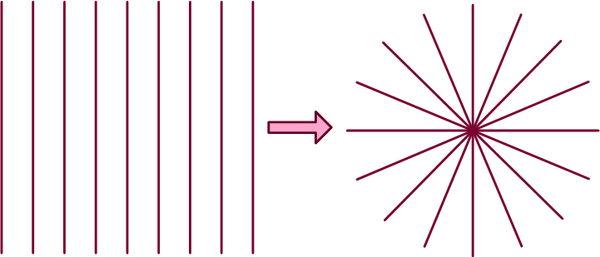
我们也知道,绝对平行的场在自然界中是不存在的,只是我们为了计算方便,在小范围内近似认为平行而已。如果把尺度放大了看,更多的场是不平行的、是发散的,所以自然界中大量存在等角螺线现象就很正常了。
例如理想状态下,流体应该是直线运动的,但在发散场和地球自转的作用下,就会像飞蛾一样走出类似等角螺线的形状,天上的台风和水中的漩涡就是这样形成的,不过实际情况远比这要复杂,只能近似这样考虑。
关于对数螺线还有一个小笑话。
对数螺线是笛卡儿在1638年发现的,雅各布·伯努利也做了研究,并发现了许多非常优美的特性,经过各种变换,结果还保持原来的样子。
他十分惊叹和欣赏这种美,要求死后自己的墓碑上一定要刻上对数螺线,以及墓志铭“纵使改变,依然故我”(eadem mutata resurgo)。
结果石匠同志误将阿基米德螺线刻了上去,雅各布九泉有知一定会把棺材掀翻的!
(╯ ̄皿 ̄)╯︵┴─┴
阿基米德螺线是这样的:
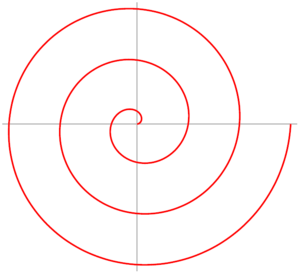
常人的确看不出区别,你能看出来吗?千万不要搞混啊!
好了!长篇大论快结束了,能坚持到这的都是Winner!下面开始讲为什么叫自然底数了。
- 对数的底数
对数中最常用的底数是10、2和e
为什么要以10为底数?
因为我们使用10进制,数量级和科学计数法也是10的倍数,例如阿伏伽德罗常数\(6.02\times 10^{23} \)。
所以\(10^{x} \)的逆运算,以10为底的对数 lg x最常用、最方便,所以又称常用对数。
10进制是数字表示法中最容易普及的,根源是我们有10个手指,人们初学数字时都喜欢借助10个手指学习1、2、3……10。到了学加减运算时,更是喜欢借助手指计算。不仅老师认为这样教学直观,学生也认为这样练习方便。通过教育,这个强大的习惯,被最广泛的传播和固化下来。但如果是8个腕足的章鱼发展出了文明,可能更喜欢8进制。
为什么要以2为底数?
因为2倍或成倍式的增长,即\(2^{x} \),是我们日常中最简单的指数式增长。我们经常说数量成倍、翻倍、翻番、翻两番,都是2倍率的增长。
你可能也发现了,前面的存款例子实际上都是\(2^{x} \),因为这样的例子最容易理解。所以\(2^{x} \)的逆运算,底数为2的对数 lb x 也会比较常见。
虽然对数的底数2和10是人们使用体验和认知体验最好的对数,但是在数学中,这两个数却是不自然的,因为都是在方便人的需要。
为什么e被称为自然底数?
用e做底数的对数表达方式是 ln x
按照古希腊哲学家的自然思想,自然是指万物的内在规律,就像自然数一样,是事物本身的属性,不以人的喜好而变化。
前面在讲“利息中的e”时,曾拿π和e做过对比。
- 边数越多越接近圆,利滚利越多越接近最大收益
- 一个对角线为1的多边形,其周长最大值是π
- 一个本金为1利率为1的存款,其存款余额的最大值是e
按照古希腊的自然思想来看:
- 对于一个完美的圆来说,π才是自然的,是圆本身的属性,尽管从数值上是一个“无理”的数。
- 对于最快速的指数增长来说,e才是自然的,这是指数增长本身的属性。
而科学家们也发现,在做数学分析时,用e做底数的对数 ln x 做计算,其形式是最简约的,用其他对数例如lg x 做计算,都会画蛇添足的多一些麻烦。
ln x 就像美学上的“增之一分则太长,减之一分则太短”。
对数学家来说,最简就是最美。这是一种纯理性的美,通过感官是无法欣赏的,只有熟悉数学的人才能深刻的感受到。这种美令无数数学家为之痴迷,虽然不会像毕达哥拉斯那样狂热,但也终其一生孜孜以求。
- 结论
- 历史上,"自然"是一种划时代的思维方法,自然还有和谐、完美的内涵
- 随着利息、对数、指数的发明,人们发现了e的存在
- 1元存1年,在年利率100%下,无穷次的利滚利就会达到e
- e和π一样都是内在规律,反映了指数增长的自然属性
- 大自然中到处都有对数螺线\(e^{\theta}\)的身影
- 其他底数都是发明出来方便人使用,只有e为底数是被发现的
- 数学家发现以e为底数的对数是计算中最简、最美、最自然的形式
把e冠以自然底数、自然常数之名,把e为底数的对数称为自然对数,是数学家们用自己的方式对e所进行的美学评价。
2004年Google公司IPO上市,创始人Larry Page和Sergey Brin决定上市融资总额为2718281828美元,也就是e的前10位数字。因为他们都精通数学,很喜欢e的自然之美,当然也希望公司能像\(e^{x}\)一样实现指数型高速增长。
Google其实是Googol的错误拼写,Googol代表\(10^{100}\)这样的天文数字,实现这样大的数看来也只能靠\(e^{x}\)指数增长了。
为什么写这个超长的文章?
因为现有的解答我都不满意,有人只说e的数学含义,有人只说自然的表层意思,不能很好的解读e与自然之间的关系。
用公式解读e当然是简洁的,但也不是我喜欢的方式,这样不仅丢失了太多有价值的信息,还会把很多人拒之门外。
我相信从大历史尺度,用生活的案例来还原e的全貌,可以让更多人来欣赏e的自然之美。耐心的读完全文,你一定会有惊喜。
#以下为补充介绍
对数为什么叫对数?
根据前面所说,纳皮尔将对数命名为Logarithm,拉丁文中logos的意思是『比率』,他用一种几何的方式发现了比例对应关系。
1653年,清代顺治年间,对数传入中国,薛凤祚与波兰传教士穆尼阁编写了《比例对数表》。康熙时的《数理精蕴》解释了『对数』中文名的来源:『对数比例乃西士若往纳白尔所作,以借数与真数对列成表,故名对数表』。
为什么对数发明早于指数?
有趣的是,历史不走寻常路,对数的发明居然是早于指数!
这就相当于先发明减法符号,再发明加法符号。
1614年,纳皮尔发明了对数和对数表。
1637年,法国数学家笛卡儿发明了指数,比对数晚了20多年。
1770年,欧拉才第一个指出:“对数源于指数”,这时对数和指数已经发明一百多年了。
我认为造成这个现象的原因有三个:
- 纳皮尔首先发现的是大数运算中有对应比例关系,这种关系可以用来简化计算,而不是考虑求指数逆运算的。
- 指数运算大家一直用,不过是用自乘的方法算。笛卡尔发明的是指数运算的符号和规则,简化了这种运算。对数和指数是不同目的下的发明,一开始人们就没有意识到两者之间的关系,直到一百多年后,欧拉才把这种互为逆运算的关系明确下来。
- 后人喜欢把容易的运算说成正运算,难的运算是逆运算,例如加法易,减法难,这是认知路径的先后造成的。
我们现代人是这样学习的:
先学指数,再学对数,指数是正运算,对数是逆运算。我们直接学习了结论,一开始就明确谁正谁逆。但其实两者互为逆运算,谁做正都行。
欧拉发现两者关系后,人们在教授数学时,为了认知体验更好,把简单的指数放到了前面,不容易理解的对数则放到了后面。
这就是后人才有的疑惑,就像亚里士多德认为利息的不自然,中国人奇怪“货币”有贝字一样,因为历史断层,我们也会惊讶于指数的发明居然会晚于对数。
后续阅读
- 干扰昆虫导航会发生什么样的趣事:《既然昆虫有趋光性,为什么昆虫不齐刷刷地奔向太阳?》
- 发明利息是处于什么样的时代背景:《为什么会有国家?》
- 无限的指数型增长会引发什么陷阱:《为什么春秋时大国间的战争还是争霸战争为主,到了战国就转向更残酷的灭国统一战争?》
- 百家争鸣是如何幻化成昙花一现的:《怎么评价重农抑商政策对中国传统社会的影响?》
推荐阅读
本文力求通俗,没用数学公式,但这样e更多的美就无法展现,目前所讲的仅仅是九牛一毛而已。在数学家的眼睛里,还可以看到e有无穷多的美妙特性。
有高等数学或数学分析基础的人可以系统阅读下面3本书:
我认为读数学史更能激发对数学的兴趣,下面的资料推荐阅读
都看到这里了,这场思想马拉松能跑下来可真不容易啊!
给这篇长文、也给自己点个赞吧!
以下是不完整参考资料,有兴趣的可以阅读
- A Brief History of Interest
- Have we caught your interest?
- A Description of The Admirable Table of Logarithms
- The Internet Classics Archive
- 那些货币金融史上的神人
- 《数学传播》- 对数与约翰.纳皮尔(John Napier)
- 中学数学与数学美
- 对数传奇:化乘为加
- 走进无限美妙的数学世界
- 纳皮尔
- e,一个常数的传奇
- 交通大学,代数学分支,对数
- 对数符号
- 几种简单平面势流的叠加势流
您尚未登录,请先登录才能评论。